梯度到底是什麽

函數在某一點沿著不同的反向移動，函數值的變化率是不同的。梯度就是一個函數的全部偏導數構成的向量，梯度向量的方向是函數值變化率最大的方向，簡單來説就是我在函數的任一點，他的梯度就表示從該點出發函數值變化最大的方向。我們可以用一個倒三角形符號（nabla，∇）表示某個函數的梯度。

假設我們現在有一個二元函數f(x,y),我們的梯度就會是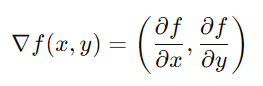
假設我們現在有一個三元函數g(x,y,z),我們的梯度就會是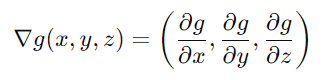

所以我們的函數接受的參數有n個的話,我們的梯度就會是分別對n個自變量求偏導數構成的n維向量：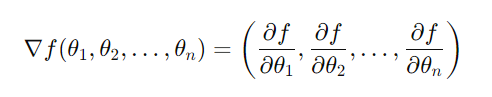

例子：
假設我們有一個函數f(x, y) = x^2 + y^2,我們的梯度就是
∇f(x, y)=(∂f(x, y)/∂x, ∂f(x, y)/∂y)=(2x, 2y)
如果我們的x=1, y=1,則梯度就會是(2,2)，這表示我們在當前位置，移動(2,2)，我的f(x,y)增長是最快的

梯度下降

那麽我們現在找到函數增長最快的方向，表示我們在梯度前加個負號，就可以往梯度的反方向移動，并且我們每次都找到梯度後，就透過當前位置減去梯度，來更新我們的位置：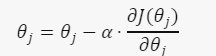

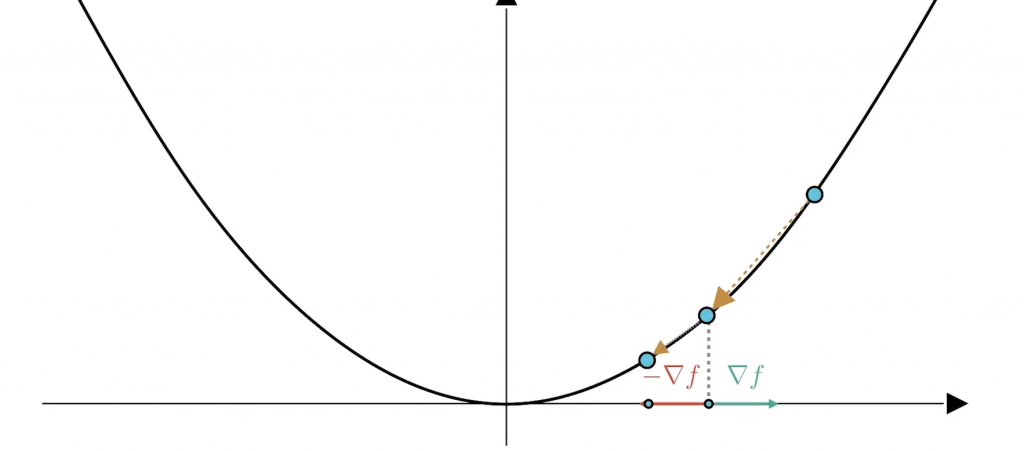
如果我們有辦法一直沿著梯度的反方向移動，那麽我們終將找到一個local minima：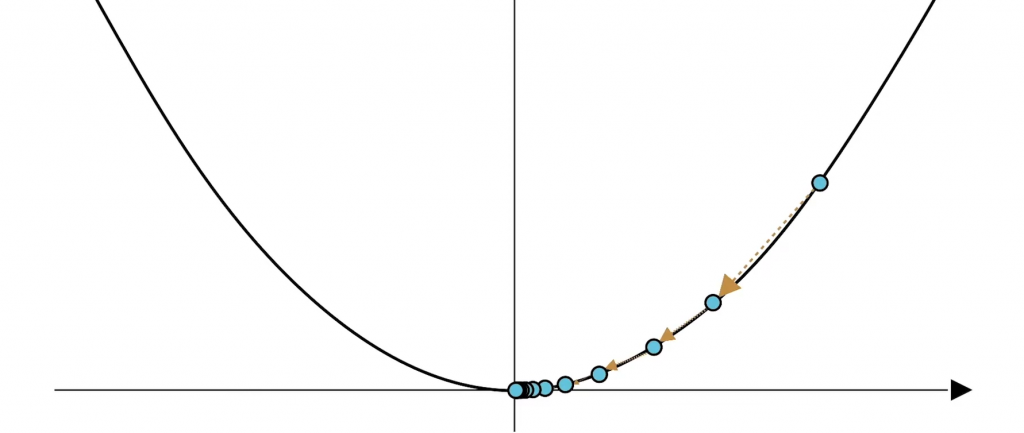

那麽現在問題來了，如果我們現在從一個點P開始去更新我們點P_i的位置，那麽我們會在谷底來回震蕩：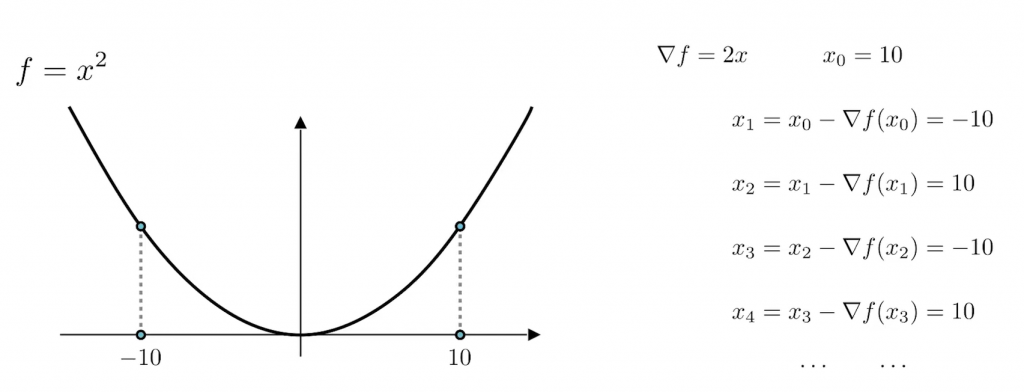

爲了解決這個問題，我們需要可以控制這個梯度的大小。我們都知道，梯度也是一個向量，一個向量分別有指向性和距離，所以我們可以透過乘上一個學習率η來控制我們的距離，但是這個學習率也不是亂調的，如果我們的學習率過大的話，就會像這樣：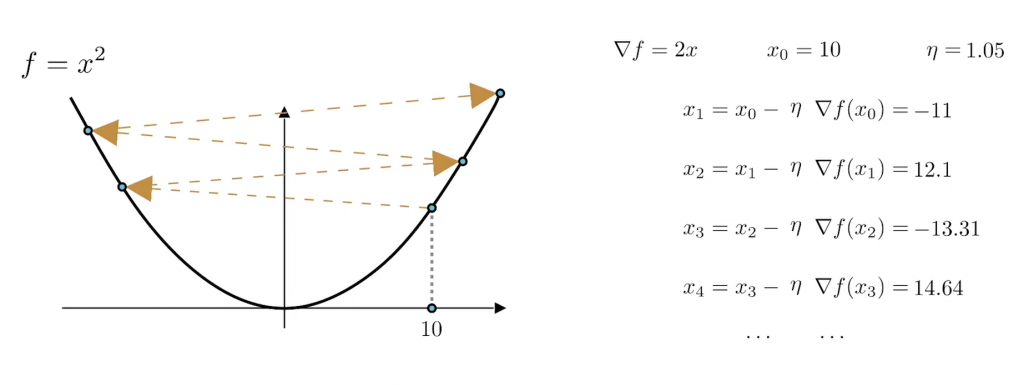

就如這張圖片所示，不僅沒有越來越接近最低點，反而還離最低點越來越遠了。

那如果將學習率調的太小，結果就會是：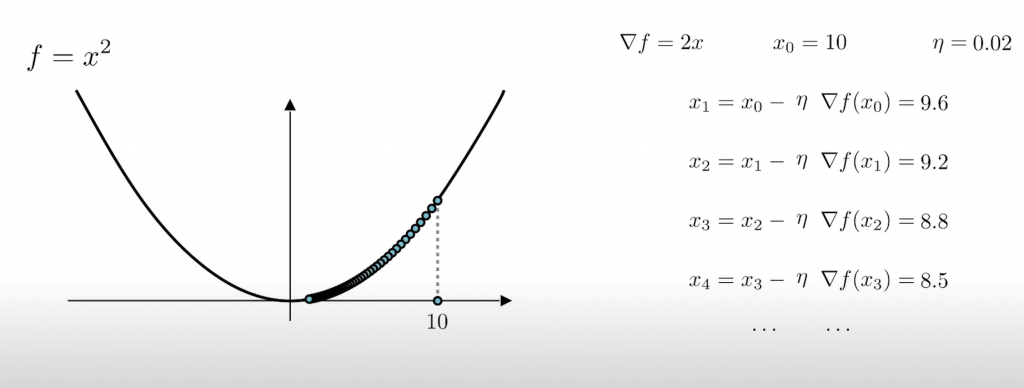

可以看到，雖然位置是在下降，但是哪怕迭代了很多次都還沒到我們的重點，所以學習率不能設太高也不能設太低。

設的剛剛好的學習率：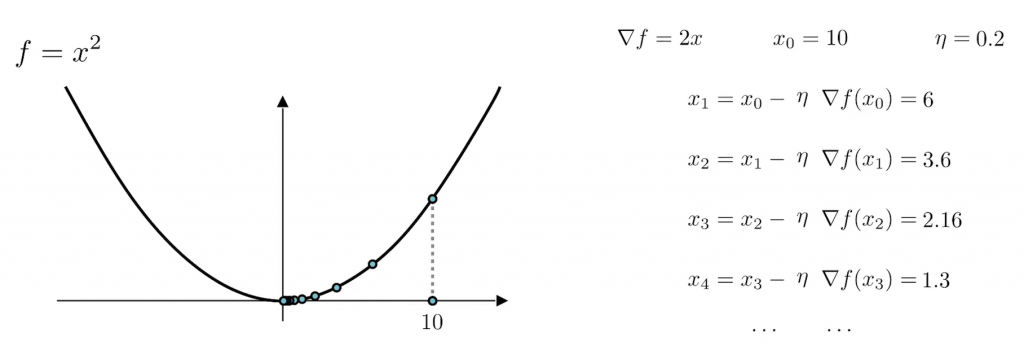

那麽現在還有一個問題，那就是我們到底要找到多小才可以停下來呢？這個是我們在跑機器學習的時候可以自己定的，我們可以給定一個數值，當我們找到的梯度小於這個數值的時候，我們就可以説，我們找到了一個good enough的權重。